======================================================================
by Guy Shaked
Also an article below! by Mr. Richard M Smith - Xerox corp:
The "canceling circles" algorithm:
As an explanation to a color intensity illusion
This article describes a new algorithm for super fast pitch detection and pitch detection in noisy waves in speech and music sound waves. It employs a new two-dimensional filter of canceling circles for recognition of main points in the sound wave.
Following, it is possible to apply two-dimensional distance measurement for estimating difference between repeating similar segments.
Further, it is demonstrated that the "canceling circles" mechanism can explain some audio-visual illusions and therefore possibly is a biologically oriented algorithm.
The C++ code of the Tishler 100 program for pitch detection The Tishler 100 program is work in progress (yet currently its not under work), it was calibrated to one specific sound wave and to be used more efficiently would need calibration for general sound waves. Regarding its accuracy - this was somewhat problematic and further work needs to be done (there are for example still bugs in the program's code unfortunately).
This is a description of a new algorithm for super fast pitch detection of speech and pitch detection in noisy speech waves. The algorithm is applicable for other waves with repeating segments, as well as visual repeating patterns.
While this algorithm is super fast - as for accuracy - further development is required (as it was only a student's project).
It makes use of a new two-dimensional filter of canceling circles for recognition of main points in the sound wave. Another innovation employed is proceeding by using two-dimensional distance measurement for estimating difference between repeating similar segments, unlike the similar correlation methods of AMDF and autocorrelation [1].
The older similar correlation algorithm : the autocorrelation algorithm was described as a "most rebust and reliable of pitch detectors" , relatively resistent to noise and was employed together with the AMDF algorithm in recent studies[2]. It seems that the fastest, most reliable and accurate "machinery" for pitch (frequency) detection - the ear-brain mechanism - uses some type of correlation [3].
Unlike "old generation" correlation algorithms , this new algorithm for pitch (frequency) detection does not employ central cliping [4], a method rarly used in our period. This is because central cliping results in ignoring in many instances a large part of the wave file, and giving emphasis to the first formants. This might result in errors as differences in a small part of the file (the first formants) might result in an interpretation of a similar pattern (different only in the examined formants) as non similar. It is even more problematic for some of the non-speech wave files where formants do not play a significant role.
The sound wave is represented visually on an X-Y axis, X being the time and Y the amplitude. The screen used is of low resolution (CGA), and 0.019 Seconds is represented in a single screen.
2.1 Controlling the Y axis (amplitude) values
The Y-axis maximum and minimum is calculated and multiplied by the required factor as to fit the maximal height of the screen.
2.2 Marking max and min points
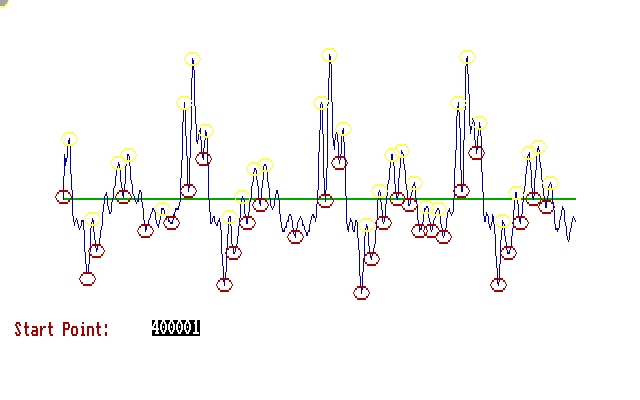
A circle of 8 pixels is painted around each maximum or minimum or shift point (shift point is defined as the last point in an horizontal section of the wave).
2.3 Finding main max-and min points
If the following conditions exist :
- The current point is a max point or a shift point heading downwards
- The last max min point (0) and that previous to it (-1) are in a distance of 8 pixels or less.
- The (-2) min max point is lower than the current point
Then the last max min point (0) and one previous to it (1) are canceled.
Also, if the following conditions exist :
- The current point is a min point or a shift point heading upwards
- The last max min point (0) and that previous to it (-1) are in a distance of 8 pixels or less
- The (-2) min max point is higher than the current point
Then the last max min point (0) and one previous to it (1) are canceled.
This can be described by the following code in C++:
//draw maximum circle 1
if ((y_prev1 > y_pix) && (y_prev1 >
y_prev2) && tip_line==1) {
flag=1;
tip_line=2;
}
//draw minimum circle 1
if ((y_prev1 < y_pix) && (y_prev1 <
y_prev2) && tip_line==2) {
flag=2;
tip_line=1;
}
//draw maximum circle 2
if ((y_prev1 > y_pix) && (y_prev1 ==
y_prev2) && tip_line==1) {
tip_line=2;
flag=1;
}
if ((y_prev1 == y_pix) && (y_prev1 >
y_prev2)) tip_line=1;
//draw minimum circle 2
if ((y_prev1 < y_pix) && (y_prev1 ==
y_prev2) && tip_line==2) {
tip_line=1;
flag=2;
}
//if two circles max min are close and touch -
erase both
if (((y_cir1 - y_cir2)*(y_cir1 - y_cir2)+(x_cir1
- x_cir2)*(x_cir1 - x_cir2)) <= 128)
{
if (((y_cir3 <= y_cir2) && (y_cir2 <=
y_prev1)) || y_cir1==y_cir3)
{
if (flag==1)
{
THEN ERASE TWO LAST MAXIMUM/MINIMUM POINTS
}
}
}
if (((y_cir1 - y_cir2)*(y_cir1 - y_cir2)+(x_cir1
- x_cir2)*(x_cir1 - x_cir2)) <= 128)
{
if (((y_cir3 >= y_cir2) && (y_cir2 >=
y_prev1)) || y_cir1==y_cir3)
{
if (flag==2)
{
THEN ERASE TWO LAST MINIMUM/MAXIMUM POINTS
} } }
The remaining max min points are the main ones of the file.
Figure 1: main minimum maximum point in a returning similar segment speech wave

Figure 2: An example of non speech section of the sound wave with main maximum minimum points
- The second main min/max point and the following main points are selected. The second main min max point is placed on the x axis in the position of the first main min max point and each of the main min max points following are placed on the x-axis in accordance to their relative position to the second.
Then the minimum distance from the shifted main min max points to the each original main min max point. If it is smaller than eleven pixels the original main min max point is canceled - meaning has found a match in the compared segment.
The above procedure for the second main min max point, is repeated for the third main point, fourth and so forth until the last point is encountered.
The number of canceled main min max points out of the overall number of main min max points represents the measure of similarity between examined segments of the wave file. If it is low than frequency was found - value of the similar returning segment distance.
So under these condition the "canceling circles" super fast version would run a 100 times faster than would the regular autocorrelation or AMDF algorithms.
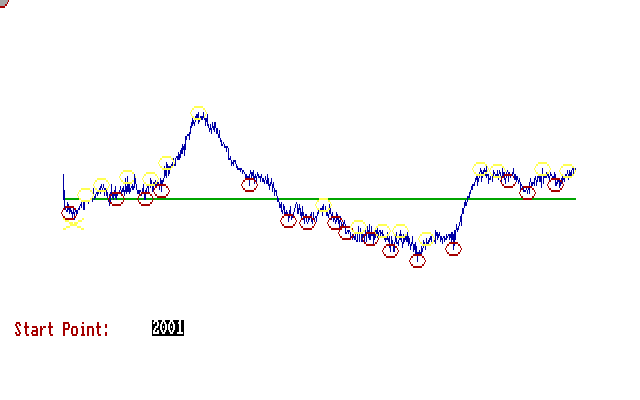
If the main points found are connected sequentially with strait lines, the folowing filtered file is created.
Figure 3: Example of a level 1 filtered file
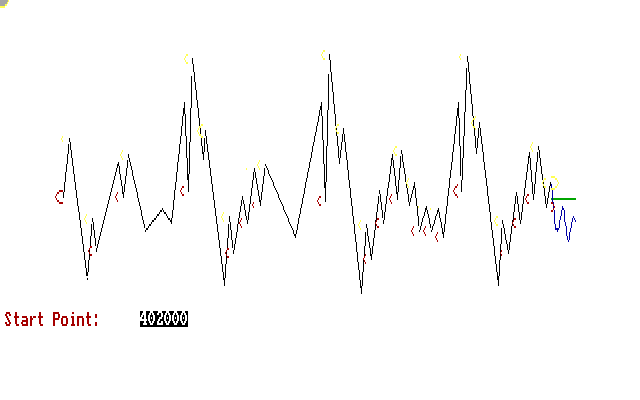
For a level 2 filtered file, each couple of main points are connected, the resulting line connecting them is then considered the x-axis and according to the lines start direction a main minimum or maximum point is searched. According to the above steps.
It is possible to repeat the steps until no new point is added. That would be an 8-pixel points final circular filter of the sound wave.
Another filtering option exists: reducing the canceling circle around the main maximum minimum points will result in a closer approximation of the sound wave.
Magnifying the canceling circle around the main maximum minimum points will result in a more general approximation of the sound wave, which might be most appropriate for formant extraction. So the size of the canceling circle point is a value to be determined in the beginning of a file filtering.
From the filtering method above a close approximation of the wave file is achieved rapidly and with low calculation complexity, with relatively small number of points to draw for the filtered sound wave (valuable for compression purposes).
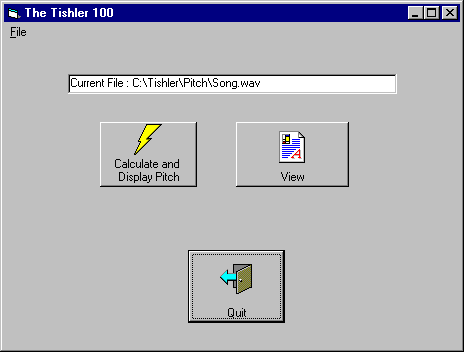
In order to display and evaluate the results of the above-mentioned algorithm, a program named the "Tishler 100" was developed in C++ and VB.
The desired result of speech and pitch detectors is an imitation of the results achieved by the human ear-brain mechanism. The most direct way in the search to achieve that goal might be to find algorithms which imitate the way the ear-brain work. The "canceling circles" algorithm represents such an approach.
Demonstrating that an algorithm imitates the ear-brain's processing of signals would have to show not only that it achieves correct results of pitch as the ear-brain does in many cases. It will also have to explain those cases in which the ear-brain fail to achieve accurate results. This is exactly what the "canceling circles" algorithm does.
Using the "canceling circles" method, some of the best known peculiarities of the Brain processing of audio-visual stimuli can be explained.
For example, the Muller-Lyer (or Mueller-Lyer) Optical Illusion.
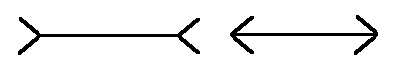
In this illusion which was devised by Franz Muller-Lyer in 1889, the left horizontal line appears longer than the right horizontal line, while physically both are equal. This affect is maximal when the fins are at a 45 (and 135) degrees (some studies show a maximal illusion at 60 [and 150], however this can be explained as depending on the fins' length)[5].
According to the "canceling circles" algorithm this phenomena is to be explained in the following way:
If circles are drawn on these three points:
1. on the begining of each fin - point A.
2. on the end of each fin - point B.
3. on the projection of each fin on the horizontal line it intersects - point C (the projection point is the one dimentional projection of the second dimention added to this figure by the fin).
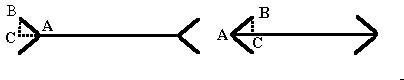
Since these circles overlap best when AC and BC are equal (so that they overlap best with point C and so are cancled), and since the projection angle near C is 90 degrees. That would mean that according to the "canceling circles" algorithm, when the fins are at 45 (and 135) degrees (meaning the angles near A and B are 45 degrees), the illusion will be maximal - as indeed happens with human perception.
The fact that point C is a result of a projection process and does not exist phisicaly, might explain that the estimate of the horizontal line is not from point C to point C' at the other end of the line, but only a little farther from point A (which is a phisical point) toward C.
While a number of other explanations to the Muller-Lyer illusion have been
suggested since it has been introduced. These explanations seem to contain
various problems. For example, the most popular explanation of the Muller-Lyer
illusion is that our brain makes mistakes about the relative depths of the
two lines. This is because we are used to seeing outside corners of buildings
with lines sloping inward away from them. There are many problems with such
an explanation. for example, buildings arrived very late in our evolution
for such a powerful mechanism (over-riding our senses) regarding buildings
to have evolved. Also somewhat problematic is the notion that estimating
our distance from where walls meet in the distance is useful for any purpose.
Another problem is that this illusion is kept also in touch, where the idea
that the genitally blind [9] would imagine lines with fins as lines of walls
meeting seems even further from logic.
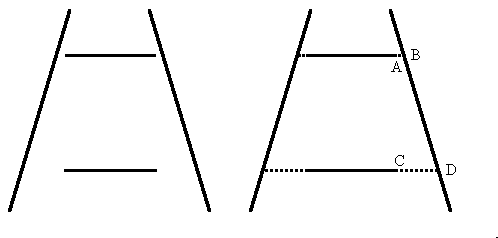
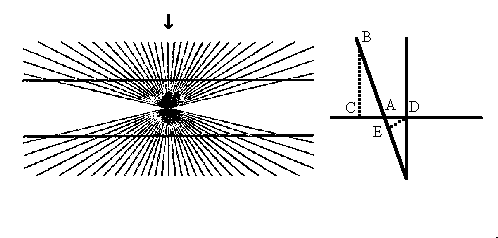
In the Ponzo illusion (above), devised by Mario Ponzo in 1913, points A and B are close enough for cancelation (and the lengthening somewhat of point A towards B) to occur between them, while points C and D are too far for cancelation, and thus the upper horizontal line is percieved as longer than the lower one.
Another illusion demonstrating the "canceling cirlcles" effect is the Poggendorff illusion (below), devised by Johann Poggendorff in 1860. In rather a similar way to what happens in the Muller-Lyer illusion, point B is canceled with point C so that the intersection with the horizontal bar is percieved as if it was more towards point A. As a result, the two segments of line crossing the horizontal bar appears to be offset.
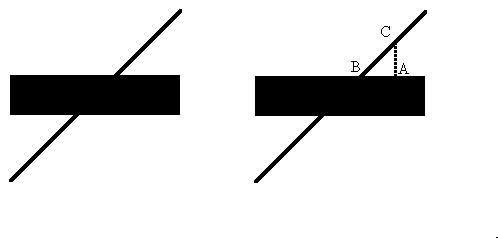
The Hering illusion (below), devised by Ewald Hering in 1861, demonstrates another aspect of the "canceling circles" algorithm. While still in a similar way to the Muller-Lyer illusion, point B is canceled with point C so that the intersection with the horizontal bar is perceived as if it was more towards point A. If we look at the intersection as if AB is the horizontal line, the result is that for line AB, D and A cancel and thus E remains, making A be perceived as if it was a bit lower (toward E) than its actually is. As a result, the line AD is perceived as not horizontal but as if point A is lower than point D. Since this is true also for adjacent sections, the whole horizontal line is perceives as not a strait line, having its peak at point D.
The following illusion of brightness-contrast, in fact allows the viewer to actually see the "canceling circles". These are visible as dark spots which appear where the white bars intersect. Their location is surrounding the edge points of the black squares, which are here the visual parallels of the minimum-maximum points in the audio sound.

It is possible therefore to conclude the illusions sections by stating that the "canceling circles" is both a viable and efficient way to process audio data, and can provide a unified explanation to numerous visual illusions (including the Muller-Lyer, Ponzo, Poggendorff, and Hering illusions).
--------------------------------------------
[1] The Tishler 100 program, uses the algorithm described in this article with another new algorithm replacing the old method of calculating the sum/average distances from the wave file
[2] Shumamura, T. & Kobayashi H., "Weighted Autocorrelation for Pitch Extraction of Noisy Speech", IEEE Trans. on Speech and Audio Processing, Vol. 9/7, 2001, p. 727
[3] Licklider, J. C. R., "Auditory Frequency Analysis", Information Theory, C. Cherry (ed.), Butterworth, London, 1956; McClellan, M.E. & Small, M. Jr., "Pitch Perception of Pulse Pairs with Random Repetition Rate", J. Acoust. Soc. Am., Vol. 41/3, 1967, pp. 690-699; Bilsen, F. A. & Ritsma, R. J., "Repetition Pitch and its Implication for Hearing Theory", Acustica, Vol. 22, 1969, pp. 63-68; Wightman, F. L., "Pattern-Transformation Model of Pitch", J. Acoust. Soc. Am., Vol. 54, 1973, pp. 407-417; Patterson, R. D. & Wightman, F. L., "Residue Pitch as a Function of Component Spacing", J. Acoust. Soc. Am., Vol. 59, 1976, pp. 1450-1460; Yost, W. A., "Models of the Pitch and Pitch Strngth of Ripple Noise", J. Acoust. Soc. Am., Vol. 66, 1979, pp. 400-411; Meddis, R., & Hewitt, T., "Virtual Pitch and Phase Sensitivity of a Computer Model of the Auditoy Priphery I: Pitch Identification", J. Acoust. Soc. Am., Vol. 89, 1991, pp. 1862-1882; Yost, W. A., Patterson, R. & Sheft, S., "A Time Domain Description for the Pitch Strength of Iterated Rippled Noise", J. Acoust. Soc. Am., Vol. 99/2, 1996, pp. 1066-1078
[4] . Medan, E. Y., & Chazan, D. "Super resolution pitch determination of speech signals", IEEE Trans. Signal Processing, ASSP-39(1):40-48, 1991
[5] Restle, E., & Decker, J., "Size of the Mueller-Lyer illusion as a function of its dimensions: Theory and data", Perception & Psychophysics, Vol. 21, 1977, pp. 489-503
[6] See footnote no. 2, above
[7] See footnote no. 4, above
[8] The human auditory mechanism recognizes pitch when at least three repetitions of similar repeating patterns occur. Olson, H. F., Music, Physics and Engineering, (2nd Ed.), New York, Dover, 1967, 460 pp
[9] That the Muller-Lyer illusion persists in touch for the congenitally blind, was demonstrated for example in: Tsai, L. S., "Muller-Lyer illusion by the blind", Perceptual & Motor Skills, Vol. 25, 1967, pp. 641-644
© 1999, 2002 (second edition)
======================================================================
by Richard M Smith
Xerox Corp.
From time to time we have observed an particular intensity difference across a printed page. In some cases it has been seen as a "left side" versus "right side" intensity difference.
The image sent to the printer consists of a full page of a uniform color, blue for example. Further, when measuring intensity of the page using either a densitometer (Optical Density or OD units), or with a spectrophotometer (delta-E, or L* units), both sides of the image have the same intensity as one would expect.
When the interface line between the two areas of perceptually different intensity is covered up (for example, by laying a narrow strip of paper over it), the illusion is gone and an observer now perceives the two sides as having the same intensity.
From knowledge of the printer design, we know of mechanisms that can create a spatial distortion in the image at the "line" between the areas perceived as having different intensities.
Over a period of years I have searched without success for information about optical illusions that are similiar to the one I have just described.
The canceling circles model is the first one I have found that might be applied to this illusion.
© 2003
| DATE | NAME | SCHOOL, UNIVERSITY | STATE, COUNTRY | FREE TEXT | SITE |
| 19 Apr 2006 | rupinder | GNE | punjab & india | this program is very helpful to me . actually i am doing work on pitch normalization for that i have to detect pitch . and there your code helped me . thanks | Physics (Acoustics) |
| 15 Feb 2006 | darshana | saurastra univercity | india-gujrat | this algorithm is really helpfull for my project .thank you very much...you have done great job. | Physics (Acoustics) |
Dear visitor, please take a short moment to sign my guest book!
----------------------------------------------------------------

shakedtg@hotmail.com Emails are
gladly received
Other articles by G. Shaked:
ART
BIBLICAL STUDIES
BIOLOGY
CINEMA
LITERATURE
MUSIC
PHILOSOPHY
PHYSICS
(ACOUSTICS)